La variable a la que se asignan valores (x en los ejemplos anteriores) se denomina variable independiente; la variable cuyo valor viene determinado por el que toma (y en los ejemplos) se llama variable dependiente o función. Decir que y es función de x equivale a decir que y depende de x.
El conjunto de valores que puede tomar la variable independiente recibe el nombre de campo de variación de la variable.
Ejemplo 1:
Y = x² - 5x + 2, x puede ser cualquier número real.
Ejemplo 2:
C= 2πr, la variable independiente es el radio r de la circunferencia. El campo de variación de r es el conjunto de todos los números positivos y el cero.
Ejemplo 3:
La población y de una nación es función del año x. El campo de variación de x está formado por los años 1880,…..1950.
La variable independiente x es el conjunto de los números reales mayores o igual a cero, lo cual se representa por x ≥ 0.
Ejemplo 4:
En la función y = ± √x, si se quiere que y siempre real, los valores que se pueden asignar a la variable independiente x es el conjunto de todos los números mayores o igual a cero, lo cual se representa por x ≥ 0.
Ejemplo 5:
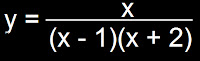En la función la variable x puede tomar cualquier valor real excepto x = 1 y x = - 2, para los cuales la función y no está definida. Por consiguiente, el campo de variación está constituido por el conjunto de los números reales excepto 1 y – 2.
No hay comentarios:
Publicar un comentario